https://openreview.net/forum?id=M752z9FKJP
Learning Strides in Convolutional Neural Networks
Convolutional neural networks typically contain several downsampling operators, such as strided convolutions or pooling layers, that progressively reduce the resolution of intermediate...
openreview.net
해당 논문을 보고 작성했습니다.
Abstract
CNN은 일반적으로 strided convolution이나 pooling layer를 사용하여 downsampling을 진행합니다. 이를 통해 중간 representation의 resolution을 점진적으로 축소시킬 수 있습니다. 이 경우, 어느 정도로 stride 할지 나타내는 중요한 hyperparameter가 존재하게 됩니다. stride라는 parameter는 미분 불가능하기에, 최적의 값을 찾기 위해서는 교차 검증 또는 discrete optimzation을 해야만 합니다. 그래서 저자들은 학습 가능한 stride를 가진 첫 번째 downsampling layer인 DiffStride를 소개합니다. DiffStride는 fourier domain에서 cropping mask 크기를 학습하며, 이를 통해 미분 가능한 방식으로 resizing을 효과적으로 수행합니다. 저자들은 audio 및 image classification에서 저자들의 방식이 효과적임을 입증합니다.
Introduction
CNN은 image classification, audio pattern recognition, text classification 등 다양한 task에서 널리 쓰이는 neural architecture입니다. CNN block으로 이루어진 convolutional layer는 input feature를 resolution은 보존하면서 더 높은 level의 표현으로 project합니다. non-linearities와 normalization layer와 같이 사용될 때, 일정한 resolution에서 풍부한 mapping을 할 수 있게 됩니다. 그러나, 많은 task는 low-level high-resolution measurement(waveform, pixel)를 통합하여 high-level low-resolution 정보(화자의 신원, 얼굴의 존재 등)를 추론합니다, 이와 같이 통합하는 것은 여러 downsampling 과정을 거쳐 관련 없는 정보를 버리면서 올바른 feature를 추출해야만 합니다. 마지막엔, pooling layer와 strided convolutions가 점진적으로 input의 resolution을 줄입니다. 이를 통해 여러 이점을 얻을 수 있습니다. 먼저, feature가 task와 관련된 정보에만 focusing하도록 만들어줍니다. 그리고 low-pass filter와 같은 pooling layer는 shift invariance를 개선합니다. 추가적으로, 줄어든 resolution은 소수점 연산량을 줄여주고 뒤에 등장하는 layer의 receptive field를 넓혀줍니다.
Pooling layer는 보통 2 단계로 분해할 수 있습니다. (1) 전체 input에 대해 densely하게 local 통계량을 계산합니다. (2) 이러한 통계를 정수 striding factor로 sub-sampling합니다. 이전 연구들은 대부분 (1)을 개선했습니다. aliasing을 피하고 local detail을 보존하고 training data 분포에 adapt할 수 있는 max or average pooling을 사용하면서 개선했습니다. 정수 striding이 너무 빠르게 resolution을 줄인다는 것((2,2) striding은 75%를 감소시킴)을 관측하고 난 후, 분수(즉, 유리수) stride를 사용하는 fractional max-pooling이 등장했습니다. 이를 통해 network에 더 많은 downsampling layer를 통합할 수 있게 되었습니다. 비슷하게, spectral pooling도 등장했는데, 이는 input을 fourier domain에서 crop하는 방식이며, 이를 통해 낮은 fequency(주로, 이미지의 기본 형태나 오디오의 기본 음색과 같은 일반적으로 더 중요한 정보를 표현. 오히려 high frequency에는 불필요한 정보 및 노이즈가 포함되기도 함)를 강조하면서 분수 stride로 downsampling을 수행합니다.
fractional stride가 downsampling layer를 디자인할 때 유연성을 제공해주었지만, 이미 거대한 search space의 크기를 더 증가시킵니다. 실제로 stride는 hyperparameter이기 때문에, 좋은 stride value를 찾는 것은 여러 실험을 통해 찾아야 합니다.
그래서 이 연구에선, 저자들은 DiffStride를 제안합니다. 이는 network를 학습할 때 stride도 동시에 학습하는 첫 downsampling layer입니다. DiffStride는 spatial domain에서의 downsampling을 frequency domain에서 cropping하는 것으로 변경합니다. DiffStride는 striding hyperparameter에 의해 정해지는 고정된 크기의 bounding box로 crop하는 대신, backpropagation을 통해 cropping box의 크기를 학습합니다. 이를 하기 위해서, 저자들은 학습 가능한 크기의 2D version attention window를 제안합니다. 저자들은 다양한 실험을 통해 DiffStride의 성능을 보여줍니다. 추가로 ResNet-18에 DiffStride를 적용하여, hyperparameter tuning 작업 없이 optimal한 실험 결과로 수렴하는 것을 보입니다.
Methods
Notations

x ∈ R^(H x W)라고 할 때, discrete Fourier Transform(DFT) y = F(x) ∈ C^(H x W)는 고정된 basis filter 집합에 대한 분해를 통해 얻어집니다. DFT transformation은 linear하고 역 DFT은 conjugate로 얻어집니다. 실수 값 signal x ∈ R^(H x W)의 fourier transform은 conjugate 대칭을 가지므로, width dimension에 대한 positive half frequency로부터 x를 구할 수 있으며 negative frequency는 생략할 수 있습니다. 추가적으로, DFT와 역 변환은 input에 대해 미분 가능하며 DFT의 도함수는 역 DFT입니다(역 DFT의 도함수는 DFT). fourier represnetation y를 input으로 받는 loss : C^(H x W) ⇒ R을 고려했을 때, x에 대한 loss의 기울기는 역 DFT를 통해 구할 수 있습니다.

식으로 표현하면 위와 같습니다.
저자들은 앞으로 등장하는 기호들을 다음과 같이 정의한다고 합니다.

Downsampling in convolutional neural networks
CNN에서 downsampling representation의 기초 mechanism은 strided convolution입니다. 이는 input을 finite impulse response filter와 convolve하고 output을 downsample합니다. 이에 대안으로, non-strided convolution을 먼저 적용한 다음 average나 max와 같은 local 통계를 계산하는 pooling을 거치는 방법이 있습니다. 이 두 가지 경우, downsampling은 input의 global structure로부터 이득을 취할 수 없으며 중요한 정보도 버릴 수 있습니다. 게다가, 정수 stride는 resolution을 크게 감소시킵니다(input dimension의 75%를 감소). 그리고 적절한 stride값을 찾는 것은 매우 번거로운 작업입니다.
Spectral pooling
자연 신호의 energy는 일반적으로 frequency domain에서 균일하게 분포되어 있지 않으며, 음성이나 이미지와 같은 signal은 대부분의 정보를 lower frequency에서 집중하고 있습니다. 이를 바탕으로 spectral pooling이 등장했습니다. 이는 spatial pooling의 정보 손실을 줄이면서 분수 downsizing factor를 사용할 수 있습니다. spectral pooling은 low frequency를 손실 없이 보존하는데, 이는 spatial/temporal convnet의 알려진 약점입니다.
저자들은 input x ∈ R^(HxW)와 stride S = (S_h, S_w) ∈ [1, H) x [1, W)로 고려합니다. 먼저 DFT는 x를 이용해 계산됩니다. 계산된 결과는 y = F(x) ∈ C^(HxW)(C는 복소수를 의)이며, 간단히 이 matrix y의 중심이 DC 성분 - zero frequency라고 가정합니다. 즉, DFT 결과를 중심 이동하여 DC 성분을 중앙에 두어, 낮은 주파수 성분이 중앙 주변에 위치하고, 높은 주파수 성분은 중앙으로부터 멀어지도록 만들어냅니다. 그다음 bounding box size는 다음과 같습니다.

왼쪽이 bounding box size입니다. 해당 크기로 matrix를 중심 주위로 자르고

오른쪽과 같이 matrix를 만듭니다.
마지막으로 해당 matrix를 다시 spatial domain으로 변환하는데, 이때 역 DFT를 사용합니다. 식은 아래와 같습니다.

실제로 사용할 때, x는 다중 channel input(i.e. x ∈ R^(HxWxC))이며, 이러한 cropping은 모든 channel에서 적용됩니다. 또한, x는 실수이고 Hermitian symmetry를 이용해 DFT 계수의 positive 부분(절반)만 계산하면 됩니다. 이를 통해 연산량과 memory를 아낄 수 있으며 output이 실수값이 되도록 만들 수 있습니다.
정수 stride를 사용하는 spatial pooling과 다르게, spectral pooling은 정수 output dimension이면 되기 때문에 더 세밀한 downsizing이 가능합니다. 게다가, spectral pooling은 전체 input에 대한 lwo-pass filter로써 역할을 하며, 이를 통해 일반적으로 가장 관련성이 높은 정보인 lower frequency를 유지하고 aliasing을 방지합니다. 그러나 spatial pooling과 마찬가지로, spectral pooling은 input에 대해 미분이 가능하지만 stride에 대해 미분할 순 없습니다. 그래서 각 downsampling layer에 적용할 hyperparameter S를 설정해야만 합니다. spectral pooling은 더 이상 정수 값으로 제한되지 않기 때문에 더 많은 경우의 수가 존재합니다.
DiffStride

적절한 striding parameter를 찾는데 어려움이 있기 때문에, 저자들은 DiffStride를 제안합니다. 이는 backpropagation을 통해 spectral pooling이 stride를 학습할 수 있도록 만든 downsampling layer입니다. x∈R^(HxW)를 downsample하기 위해서, DiffStride는 spectral pooling처럼 fourier domain에서 crop합니다.
그 대신 spectral pooling은 고정된 크기의 bounding box를 사용하여 crop하지만, DiffStride는 box size 또한 backpropagation을 이용해 학습합니다. 학습 가능한 box W는 input shape와 smoothness factor R, stride에 의해 매개변수화됩니다. mask W를 미분 가능한 두 개의 1D masking function의 외적으로 만들어내며(위 그림과 같이), 하나는 수직 축이고 하나는 수평축입니다. 이러한 1D mask는 adaptive attention span을 이용해 직접적으로 만들어집니다. 계수의 conjugate 대칭을 활용하여, horizontal 축의 positive frequency만 고려하며, vertical mask는 zero frequency를 중심으로 mirroring합니다. 그러므로 두 mask는 다음과 같이 정의됩니다.

S = (S_h, S_w)는 stride를 의미하며, R은 mask의 smoothness를 조절하는 hyperparameter입니다. 이제 이 두 1D mask를 외적하여 2D 미분 가능한 mask W를 만들 수 있습니다.

이렇게 생성한 W를 2가지 방법으로 사용할 수 있습니다. (1) element-wise product를 통해 input의 fourier representation으로 사용할 수 있으며, 이는 low-pass filtering 역할을 합니다. (2) mask가 zero fourier coefficient는 crop합니다.
(1)은 stride S에 대해 미분 가능하지만, cropping 연산은 미분할 수 없습니다. 그러므로, 저자들은 cropping하기 전에 mask에 stop gradient operator를 사용합니다. 이를 통해 gradient는 미분 가능한 low-pass filtering 연산을 통해 stride로 전달되지만, 미분 불가능한 cropping에는 전달되지 않습니다. 마지막으로, crop된 tensor는 역 DFT를 통해 spatial domain으로 다시 변환됩니다. 모든 이러한 단계는 아래와 같은 algorithm 1으로 요약하여 표현할 수 있습니다.

학습할 때, stride S = (S_h, S_w)가 [1, H) x [1, W) 내에 있도록 제한합니다. x가 multi-channel input의 경우(x ∈ R^(HxWxC)), channel 별로 모두 동일한 spatial dimension을 갖도록 만들기 위해 모든 channel에 대해 동일한 stride S를 학습합니다. spatial pooling과 spectral pooling은, stride가 일반적으로 spatial axes를 따라 연결됩니다(i.e. S_w = S_h). DiffStride도 학습 가능한 단일 stride를 모든 dimension에 공유함으로써 이를 수행할 수 있습니다. 그러나, 각 vertical 축과 horizontal 축에 맞는 특정 stride를 학습하는 것이 audio의 frequency representaion과 image classification 실험에서 더 좋은 결과를 가져다주었습니다. 각 downsampling layer에 hyperparameter R를 추가하는 것은 결국 여전히 hyperparameter가 존재함을 의미합니다. 그래서, 모든 layer에 동일한 R 값을 사용할 뿐만 아니라, 저자들은 각 layer에 다른 R 값을 사용하더라도 큰 차이가 없음을 알아냈습니다. 저자들은 실험에서 R = 4로 설정하고 진행했습니다. 2D case에 focusing했지만, 단일 1D mask를 사용하면 1D CNN에서 DiffStride를 사용할 수 있습니다. 그리고 3개의 1D mask에 대한 외적을 적용하면 3D input에 대한 DiffStride도 적용할 수 있습니다.
Residual block with DiffStride

l번째 layer의 output만 l+1번째 layer에 feed하는 system과 다르게 ResNet은 skip-connection을 사용합니다. skip-connection은 main branch와 동시에 연산을 진행합니다. ResNet은 2 종류의 block을 stack합니다. (1) input channel 차원과 spatial resolution을 유지하는 identity block (2) output channel dimension을 증가시키지만 strided convolution을 이용해 spatial resolution은 감소시키는 shortcut block으로 이루어져 있습니다. 저자들은 DiffStride를 이러한 shortcut block에 사용합니다. strided convolution을 stride하지 않는 convolution을 변경하고 뒤에 DiffStride를 추가하여 구현합니다. 추가적으로, main branch와 residual branch에 동일한 DiffStride를 공유하여 각 output이 동일한 크기의 spatial dimension을 갖도록 만들어줍니다.
Regularization computation and memory cost with DiffStride
network에 있는 activation 수는 stride에 의존되며, 이러한 parameter을 학습하는 것은 architecture의 공간 및 시간 복잡도를 미분 가능한 방식으로 제어할 수 있게 합니다. 이는 이전 연구와 대조적이며, model의 parameter에 대해 일반적으로 미분 불가능한 복잡도 측정치(e.g. 소수점 연산 수(FLOPs))와 달리, 효율적인 architecture를 찾는 것은 high-level exploration(e.g. 분리 가능한 convolution 도입), architecture 탐색 또는 복잡도의 연속적 완화 사용(continuous relaxations of complexity)을 통해 수행됩니다.
정사각 kernel size K^2를 갖고 C'차원의 output channel을 가진 기본 2D convolution은 K^2 x C x C' x H x W 만큼의 연산량이 듭니다(이때 input x ∈ R^(HxWxC)). 이때 저장해야 하는 activation 수는 C' x H x W입니다. channel과 kernel size을 고정하면, 연산량과 convolution layer의 메모리 사용량을 input size인 H x W로 만들 수 있습니다.
DiffStride의 관점에서 l번째 layer의 input size는 다음과 같습니다.
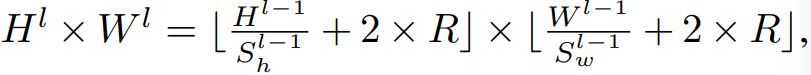
위 식은 이전 layer의 stride S^(l-1)로 미분 가능한 형태입니다. 추가적으로, input size는 이전 layer의 spatial dimension에 의해 결정되며, 해당 spatial dimension 또한 본인들의 이전 layer의 spatial dimension에 의해 결정됩니다. layer에 대한 귀납을 통해 최종 연산량과 메모리 사용량은 다음 식에 비례합니다.

DiffStride의 관점에서 kernel size와 channel 수는 training동안 상수로 남기 때문에, training loss에 정규화 항을 추가함으로써 model을 시간 및 공간 효율성 측면에서 직접적으로 정규화할 수 있습니다. 정규화 항은 다음과 같습니다.
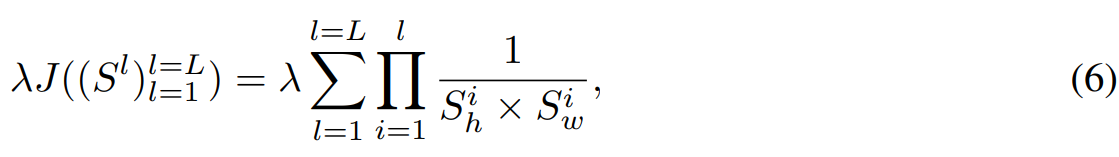
여기서 λ은 정규화 weight입니다.
Experiments
저자들은 8개 task에서 DiffStride의 성능을 평가합니다. 동일한 구조에서 strided convolution만 no stride convolution followed by DiffStride로 변경해서 비교합니다. 또한 spectral pooling의 결과와도 비교합니다.
Audio classification
저자들은 5가지 task에서 성능을 비교합니다. 음향 장면 분로, 새소리 감지, NSynth dataset에서 음악 악기 분류 및 피치 추정, 음성 명령 분류입니다. 16kHZ로 sample된 audio를 64 channel의 mel-spectrogram으로 분해하며, 25ms의 window를 사용하여 매 10ms마다 계산됩니다.
2D CNN 기반 model은 spectrogram을 input으로 받습니다. 그리고 시간에 따라 (3x1) kernel을 사용하는 strided convolution block과 주파수에 따라 (1x3) kernel을 사용하는 strided convolution block을 번갈아 배치합니다. 각 strided convolution 뒤에는 ReLU와 batch normalization이 붙습니다. channel dimension의 순서는 (64, 128, 256, 256, 512, 512)이며 stride는 ((2,2), (2,2), (1,1), (2,2), (1,1), (2,2))순서로 설정합니다. CNN의 output은 global max-pooling을 지나고 단일 linear classification layer에 들어갑니다. multi-task classification의 경우엔 multiple classification layer를 사용합니다.

결과표는 다음과 같습니다. single task의 acoustic scene을 제외하면, DiffStride는 strided convolution과 spectral pooling의 성능을 뛰어넘습니다.

위 표는 model에 존재하는 첫 layer의 DiffStride에서 학습된 stride 값을 의미합니다. 초기 설정된 stride는 (2,2)였는데, 그 값을 벗어나 학습된 것을 볼 수 있습니다.
Image classification
저자들은 ResNet-18을 사용하여 strided convolution, spectral pooling, DiffStride를 비교했습니다. 저자들은 ResNet-18에 존재하는 shortcut block의 stride를 1~3 사이로 랜덤하게 6개 sampling하여 적용했습니다. 저자들은 CIFAR10, CIFAR100 dataset을 이용합니다. CIFAR10은 10개의 class가 존재하며, 각 class마다 6000장의 32x32 image가 존재합니다. 그래서 저자들은 50000장은 train, 10000장은 test에 사용합니다. CIFAR100은 CIFAR10과 동일한 image data를 사용하지만, 좀 더 자세하게 labeling하여 100개의 class가 존재합니다. 그리고 ImageNet dataset으로도 성능을 확인합니다. ImageNet dataset은 1000개의 class로 구성됩니다. ImageNet datset에 존재하는 128만 개의 image로 train하고, 5만 개의 validation set을 사용합니다.

위 table은 CIFAR dataset에 대한 실험 결과입니다. 실험 결과를 보면 알 수 있듯이, hyperparameter stride는 매우 중요합니다. 어떻게 설정하는지에 따라 실험 결과가 매우 달라집니다. spectral pooling이 좋지 않은 초기화 상태에서 strided convolution보다 더 강건한 모습을 보인다는 걸 알 수 있습니다. DiffStride는 좋지 않은 stride초기화값에서도 전체적으로 훨씬 더 강건한 모습을 보이며, 일관되게 높은 정확도로 수렴합니다. 즉 DiffStride는 stride를 학습 중에 찾을 수 있도록 만들었기 때문에, 6561번 실험을 통해 좋은 stride를 찾는 것보다 더 효율적이라는 것을 알 수 있습니다.
Conclusion
저자들이 제안한 DiffStride는 학습 가능흔 stride를 사용하는 첫 downsampling layer입니다. DiffStride를 audio와 image classification에 적용하여 cross-validating stride를 제거했습니다. 저자들의 방식은 stride를 학습하여 pooling layer를
효과적으로 적용할 수 있음을 보였습니다.
'연구실 공부' 카테고리의 다른 글
| 음성학 관련 공부 (0) | 2024.02.27 |
|---|---|
| spectrum, spectrogram, Mel-spectrogram, MFCC (0) | 2024.02.27 |
| [논문] Learning Transferable Visual Models from Language Supervision (0) | 2024.02.22 |
| [논문] LoRA: Low-Rank Adaptation of Large Language Models (0) | 2024.02.20 |
| [논문] Deep Residual Learning for Image Recognition (0) | 2024.02.19 |



