[논문] Auto-Encoding Variational Bayes

https://arxiv.org/abs/1312.6114

Auto-Encoding Variational Bayes

해당 논문을 보고 작성했습니다.

 

Abstract

연속 잠재 변수를 가진 확률 모델에서, 다루기 어려운 posterior 분포와 큰 dataset이 존재할 때, 어떻게 효과적으로 추론하고 학습할 수 있을까? 해당 논문에서는 큰 dataset에서도 동작하고, 복잡하지 않은 미분 조건에서는 다루기 어려운 경우에도 적용 가능한 확률론적 변분추론과 학습 algorithm에 대해 소개합니다. 해당 논문에는 크게 2가지 contribution이 있습니다. 첫째, variational lower bound의 재매개변수화가 standard stochastic gradient 방법을 사용하여 직관적으로 최적화될 수 있는 하한 추정기를 제공한다는 것을 보여줍니다. 두번째로, data point당 continuous latent variable(연속 잠재 변수)를 가진 independent하고 identical한 dataset의 경우, 추정 불가능한 posterior에 대해 근사 추론 모델(인식 모델)을 제안된 lower bound estimator를 사용하여 posterior 추론을 효율적으로 수행할 수 있음을 보입니다. 

 

Introduction

continuous latent variable 또는 parameter가 추적 불가능한 posterior distribution을 가질 때, directed probabilistic model을 어떻게 근사 추론하고 학습을 할 수 있을까? variational Bayesian(VB) 접근법은 추적 불가능한 posterior에 대한 근사치를 최적화하는 것을 포함합니다. 하지만, 일반적인 mean-field 접근법은 근사 posterior에 대한 기대값의 분석적 해답을 요구하는데, 추적 불가능한 경우가 일반적입니다. 그래서 저자들은 어떻게 variational lower bound의 재매개변수화가 단순하고 미분 가능하며 편향되지 않은 lower bound estimator를 얻는지 보입니다. 이러한 SGVB(Stochastic Gradient Variational Bayes) estimator는 continuous latent variable이나 parameter를 가진 거의 모든 모델에서 효율적인 근사 posterior inference를 위해 사용될 수 있고, standard stochastic gradient ascent를 이용해 최적화할 수 있습니다.

independent하고 identical한 distribution을 가진 dataset과 datapoint 당 continuous latent variable을 가진 경우, auto-encoding VB(AEVB) algorithm을 제안합니다. AEVB algorithm에서는 SGVB estimator를 사용하여 인식 모델을 최적화함으로써 추론과 학습을 특히 효율적으로 수행합니다. 이 인지 모델은 간단한 sampling을 사용하여 매우 효율적인 근사 posterior 추론을 할 수 있게 해줍니다. 이를 통해 비싸고 반복적인 추론 체계(예: MCMC)없이도 효율적으로 model parameter를 학습할 수 있습니다.

 

Method

연속적인 잠재 변수를 가진 다양한 방향 그래픽 모델들에 대한 하한 추정기(stochastic objective function)를 유도하는 방식을 보겠습니다. 일단 저자들은 datapoint마다 잠재변수가 존재하는 i.i.d dataset이라고 제한한 상태에서 global parameter에 대한 maximum likelihood 또는 maximum a posterior 추론을 수행하고, 잠재 변수에 변분 추론을 수행합니다.

 

예를 들어, global parameter에 대한 변분 추론을 한다고 확장해보겠습니다.

 

- Problem scenario

N개의 i.i.d. sample로 이루어진 dataset X를 고려합니다. data가 random process에 의해 생성되고, 관측하지 못하는 연속적인 random 변수 z를 포함하고 있다고 하겠습니다. random process는 2가지 step으로 이루어집니다. 먼저 random 변수 z는 prior 분포 P_Θ*(z)에 의해 생성됩니다. 그 다음 value x는 조건부 확률 P_Θ*(x|z)에 의해 생성됩니다. 우리는 prior P_Θ*(z)와 likelihood P_Θ*(x|z)가 P_ Θ(z)와 P_ Θ(x|z)라는 매개변수화된 두 분포에서 왔다고 볼 수 있으며, 그들의 PDF(Probability Density Function)은 Θ와 z에 대해 거의 모든 공간에서 미분 가능하다고 합니다. 하지만, 이 과정의 많은 부분들을 우리가 볼 수 없습니다. Θ*와 잠재 변수 z의 값을 알지 못합니다.

저자들은 marginal or posterior probabilities에 대한 단순화 과정을 하지 않습니다. 저자들은 일반적인 algorithm을 통해 효과적으로 동작하게 만듭니다.

 

    1. Intractability(불가능성): marginal likelihood P_Θ(x) = ∫P_Θ(z)P_Θ(x|z)dz이 불가능한 경우(likelihood를 평가하거나 미분하지 못하는 경우, 여기에서는 모든 z에 대해 적분하는 것 자체가 불가능한 상태), 진짜 posterior density P_Θ(z|x) = P_Θ(x|z)P_Θ(z) / P_Θ(x) 가 불가능한 경우(EM algorithm을 사용하지 못하는 경우, 우리는 P_Θ(x)를 구하지 못하는 상태이므로 이 또한 구할 수 없는 상태), 그리고 어떤 합리적인 mean-field VB algorithm도 불가능한 경우를 의미합니다. 이러한 불가능성은 꽤나 흔하고, 어느정도 복잡한 likelihood function P_Θ(x|z)의 경우에 나타납니다.

 

    2. A large dataset: 너무 많은 data를 가지고 학습을 한다면 batch 단위 optimization을 하는 것이 너무 큰 cost가 소모됩니다. 그래서 저자들은 작은 minibatch를 사용해 parameter를 update하거나, single datapoint를 이용해 parameter를 update합니다. 하지만 Monte Carlo EM와 같은 sampling 기반 방식들은 각 datapoint마다 일반적으로 비용이 많이 드는 sampling loop를 포함하기 때문에 매우 느립니다.

 

저자들은 위와 같은 scenario에서 제시된 3 가지의 문제를 해결하는 방법을 제시합니다.

 

    1. parameter Θ를 위한 효율적으로 ML or MAP 근사하기. parameter를 효율적으로 구하게 된다면, 숨겨진 random process를 모방할 수 있고 실제 data와 유사한 data를 생성할 수 있습니다. parameter Θ의 경우, P_Θ(x|z)에 사용되며, 이는 decoder 부분의 parameter이기 때문에 실제 data와 유사한 data를 생성할 수 있다고 합니다.

 

    2. parameter Θ를 선택하기 위해 관측된 value x가 주어졌을 때, latent variable z의 posterior inference를 효율적으로 근사하기. 이는 코드를 작성하거나 data를 표현하는 task에서 유용합니다. z의 posterior의 경우, encoder 부분에 해당하기 때문에 가능합니다.

 

    3. 변수 x의 marginal inference를 효과적으로 근사하기. 이를 통해 prior P(x)가 요구되는 모든 종류의 inference task에서 동작하게 됩니다. 이를 이용하면 computer vision 분야의 경우, noise 제거, inpainting 그리고 super resolution이 가능해집니다. 

 

위에서 언급한 문제를 해결하기 위해, recognition model q_Φ(z|x)에 대해 보겠습니다. q_Φ(z|x)는 true posterior P_Θ_(z|x)를 근사합니다. mean-field variational inference에서 posterior를 근사하는 것과 다르게, q_Φ(z|x)는 필수적으로 factorial(latent variable들이 서로 독립)일 필요 없고 parameter Φ는 closed-form expectation으로 구해지지 않습니다. 대신에, 저자들은 생성 모델 parameter Θ과 recognition model parameter Φ을 동시에 학습하는 방식을 소개합니다.

코딩 이론 관점으로 봤을 때, 관측되지 않은 변수 z는 latent representation 또는 code로 해석될 수 있습니다. 그러므로 이 논문에서는 recognition model q_Θ(z}x)을 확률적 encoder로 사용합니다. 왜냐하면 datapoint x가 주어지면, 주어진 datapoint x를 생성할 수 있는 code z가 가능한 value들의 분포를 생성하기 때문입니다. 유사하게, 가능한 x의 값들의 분포를 z가 생성할 수 있기 때문에 p_Θ(x|z)을 확률적 decoder로 볼 수 있습니다.

 

- The variational bound

marginal likelihood는 각각의 datapoints의 marginal likelihood의 합으로 구성됩니다.

 

 

왼쪽 식을 오른쪽 식으로 다시 쓸 수 있습니다. 일단 우변의 첫번째 항은 근사 posterior distribution과 true posterior distribution의 KL divergence를 의미합니다. KL divergence는 음수 값을 갖지 않기 때문에, 우변의 두번째 항은 datapoint i의 marginal likelihood의 (variational) lower bound 라 부를 수 있습니다. 그리고 이 식을 다시 바꿔 쓸 수 있습니다.

 

다시 보면 KL divergence는 음수 값을 갖지 않기 때문에 log P_Θ(x^(i)) 값이 lower bound보다 크거나 같게 됩니다. 저자들은 lower bound를 variational parameter Φ과 generative parameter Θ에 대해 미분하고 최적화하길 바랍니다. 하지만, Φ에 대한 기울기가 문제입니다. Monte Carlo gradient estimator를 사용하면, gradient estimator가 매우 높은 분산을 나타내며, 저자들의 목적에는 실용적이지 않습니다(Monte Carlo의 경우 여러번 sampling하여 평균을 구하는 방식이므로, 분산이 커질 수 있습니다).

 

일단 논문에서는 위와 같은 설명을 해주었지만, 다시 차근차근 살펴보겠습니다.

 

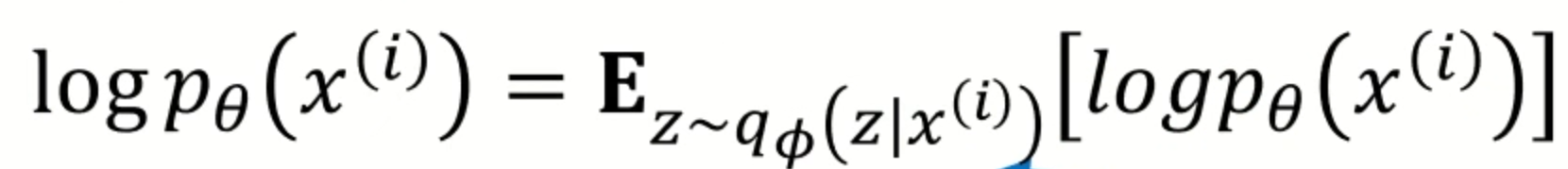
우리가 가정한 encoder와 decoder를 이용해 위와 같은 식으로 나타낼 수 있습니다. 위 식에서 p_Θ(x)의 경우, bayes rule에 따라 p_Θ(x|z)p_Θ(z) / p_Θ(z|x) 로 표현할 수 있습니다. 이를 적용하고 분모와 분자에 같은 값을 곱해주면

 

위와 같은 식이 됩니다. log의 경우 곱셈은 덧셈으로 분해가 가능하고, 나눗셈은 뺄셈으로 분해가 가능합니다. 이를 이용해

 

위와 같이 표현할 수 있습니다. 두번째 항의 expectation 부분을 전개하겠습니다. ∫_z (log(q_Φ(z|x)/p_Θ(z))q_Φ(z|x) dz)와 같은 형태로 표현할 수 있습니다. 이는 KL divergence공식과 같은 형태이며 세번째 항에도 적용한다면 아래와 같은 식이 작성됩니다.

 

이와 같이 log(p_Θ(x^(i))를 표현할 수 있습니다. 저자들이 말한 것과 같은 형태로 식이 등장하게 됩니다. 여기서 세번째 항을 보면 우리는 p_Θ(z|x^(i))에 대한 연산을 진행할 수 없습니다. 왜냐하면 p_Θ(z|x^(i)) = p_Θ(x^(i)|z)p_Θ(x) / p_Θ(x^(i)) 이고 여기선 또 p_Θ(x^(i))를 구하지 못하기 때문에 p_Θ(z|x^(i))를 다룰 수 없습니다. 하지만 KL divergence의 값은 항상 0 이상의 값을 갖는다는 것을 알기 때문에 무시하고 첫번째 항과 두번째 항을 묶어 lower bound라고 표현한 것입니다. 이제 우리가 처음에 구하려고 했던 log p_Θ(x)는 항상 lower bound보다 크거나 같은 형태가 됩니다. 결국 우리는 log p_Θ(x)  

를 maximize하도록 하는 Φ와 Θ를 찾기 위해 lower bound를 maximize하는 parameter를 찾는 방식으로 진행하면 됩니다. 하지만 Φ의 경우 문제가 됩니다. Monte Carlo gradient estimator를 통해 기울기를 구하려고 할 때, 분산이 매우 크다는 문제가 존재합니다.

 

- The reparameterization trick

저자들은 문제를 해결하기 위해 q_Φ(z|x)로부터 sample을 생성하는 새로운 방법을 도입했습니다. 필수적인 parameterization trick은 꽤나 간단합니다. z를 continuous random variable이라 보고 z는 q_Φ(z|x)라는 조건부 확률 분포에서 sampling되었다고 하겠습니다. 이와 같이 표현된다면 random variable z는 g_Φ(ε, x)로 표현할 수 있습니다. 여기서 ε은 독립적인 marginal probability를 가진 보조 변수이고, g_Φ는 Φ라는 parameter로 이루어진 function입니다.

reparameterization을 적용한다면, q_Φ(z|x)를 Monte Carlo estimate을 Φ로 미분가능하게 됩니다. 일단 f(z)의 g_Φ(z|x)에 대한 mote Carlo expectation estimate는

 

이와 같습니다. 이걸 lower bound에 적용시킨다면

 

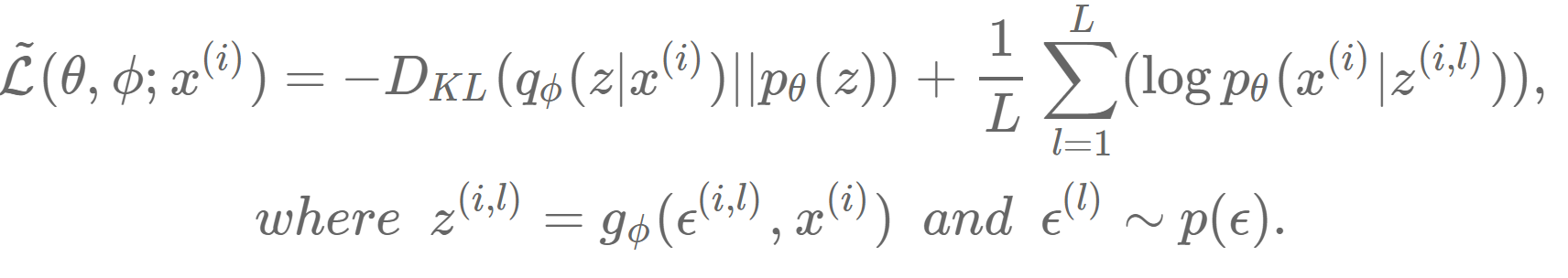
이와 같은 형태로 변하게 됩니다. 이 전에는 z가 q_Φ(z|x)에서 직접 sampling되는 형태였으며, 미분이 불가능했습니다. 하지만 위와 같이 변형한다면 미분이 가능합니다. 예를 들어 p(z|x) ~ N(μ, Σ)일 때, 과거에는 distribution에서 바로 z를 sampling했다면, 이제는 ε ~ N(0, 1)에서 ε를 구하고 z = μ + σε의 형태로 나타낼 수 있게 됩니다. 이를 통해 직접 distribution에서 sampling하는 것이 아니고, (μ, Σ)에 대해 미분 가능한 형태가 됩니다.

이 전에 sampling을 하는 방식은, 결국 확률 분포에서 sampling하는 것이고 이는 stochastic하며 continuous하지 않기 때문에 미분 불가능했습니다. 즉 backpropagation 자체가 불가능했습니다. 그래서 저자들은 reparameterization trick을 사용해 sampling 과정을 미분 가능하도록 만들었습니다.

이와 같이 reaparameterization trick을 이용한다면 미분 불가능한 형태인 sampling을 미분 가능하도록 표현할 수 있게 됩니다. 저자들은 어떤 미분 가능한 함수 gΦ()를 사용해야 하며, 어떤 ε을 사용해야 하는지에 대한 3가지 기초적인 설명을 해주었습니다.

 

 

- The SGVB estimator and AEVB algorithm

이번 section에서 저자들은 lower bound의 실용적인 estimator를 소개하고 parameter에 대한 미분하는 방법을 소개합니다. 저자들은 posterior를 q_Φ(z|x) 형태로 근사했지만, x를 고려하지 않은 형태인 q_Φ(z)에도 적용가능하다 합니다.

일단 approximate posterior q_Φ(z|x)를 reparameterize하여 미분가능한 transformation g_Φ(ε, x)와 noise variable ε를 사용해 z^ ~ q_Φ(z|x)로 표현할 수 있습니다.

이제 Monte Carlo estimate를 q_Φ(z|x)에 관한 어떤 함수 f(z)의 expectation에 적용하겠습니다.

 

reparameterization trick을 이용하면 위와 같은 식으로 Monte Carlo estimate를 expectation에 적용할 수 있습니다.

이를 아래에 식에 적용해보겠습니다(lower bound).

lower bound에 적용한다면 위와 같은 식을 얻을 수 있습니다. 이는 일반적인 stochastic gradient variational bayes estimator의 모습입니다. 보면 기존 lower bound의 log(p_Θ(x|z)) 부분을 Monte Carlo로 형태로 변환한 모습을 볼 수 있습니다. L 값에 따라 sampling 횟수가 정해지고, sampling된 결과의 평균으로 approximate하는 형태인 것을 볼 수 있습니다.

 

저자들은 이와 같이 minibatch를 적용해 학습하는 과정을 보여줍니다. M은 batch size이며, M이 충분히 크다면(저자들은 100 이상을 이야기했습니다) L을 1로 설정해도 된다고 합니다. 즉 Monte Carlo estimator를 1회 실행하여 하나의 sample에 대한 값을 근사한다는 것입니다. ELBO 식을 이용한 표현은 아래에 나와있습니다.

 

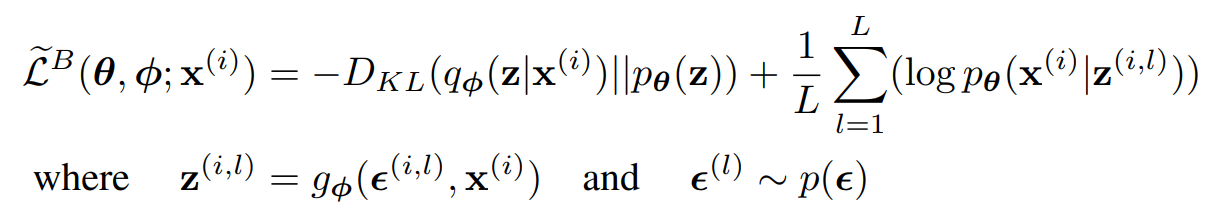
이번엔 lower bound의 KL divergence항을 보겠습니다. 이 항은 종종 통합될 수 있으며, 그로 인해 E(log(p_Θ(x|z)))만 reconstruction error로 사용됩니다. KL divergence항은 Φ를 regularization하는 역할을 하며, approximate posterior q_Φ(z|x)가 prior p_Θ(z)에 가까워지도록 합니다. prior와 가까워지도록하면, overfitting을 방지할 수 있고 prior 정보를 최대한 잘 표현하는 encoder를 만들 수 있다고 합니다.

저자들은 KL divergence을 이용하여 일반적인 estimator보다 변동성을 적은 estimator를 사용합니다. 식은 위와 같습니다.

 

이제 N개의 datapoint로 이루어진 dataset X로부터 여러 개의 datapoint가 주어졌을 때, 저자들은 full data의 marginal likelihood lower bound를 minibatch를 이용해 위와 같이 정의합니다. minibatch X^M은 총 N개의 datapoint로 이루어진 전체 dataset X로부터 M개의 datapoint를 random하게 sample하여 얻어집니다. 저자들은 실험을 통해 minibatch size M이 100과 같이 충분히 큰 상황에선, datapoint를 sample하는 횟수인 L을 1로 두면 충분하다 합니다. SGD나 Adagrad를 통해 optimize를 진행했다 합니다.

 

위 식을 다시 한번 더 살펴보겠습니다. KL divergence term은 approximate posterior distribution을 regularize하는 regularizer로 사용되고, 두 번째 항은 reconstruction error를 의미합니다. g_Φ라는 function은 datapoint x와 random noise vector ε가 approximate posterior로 mapping되도록 합니다. 

 

다시 말해 위와 같은 형태입니다. 그 이후 sample인 z는 log p_Θ(x|z)에 input으로 들어갑니다. 이 function log p_Θ(x|z)은 z가 주어진 generative model에서 datapoint x의 확률 밀도와 동일합니다. 이 항은 auto-encoder에서 reconstruction error에 해당되는 부분입니다.

 

Example: Variational Auto-Encoder

이제 encoder를 neural network로 사용하는 예시를 보겠습니다. q_Φ(z|x)는 generative model p_Θ(x|z)의 approximate posterior이며, parameter Θ, Φ는 AEVB algorithm으로 동시에 최적화됩니다.

latent variable의 prior p(z)는 isotropic multivariate Gaussian p_Θ(z) = N(z, 0, I)으로 가정합니다. 이 경우, prior는 parameter가 존재하지 않게 됩니다. 저자들은 p_Θ(x|z)를 실제 데이터의 경우 multivariate gaussian로 설정하고  이진 데이터의 경우 Bernoulli로 설정하며, distribution의 parameter는 MLP(fully connected neurla network with a single hidden layer)을 통해 z로 부터 구해집니다. true posterior p_Θ(z|x)는 구할 수 없는 형태입니다. q_Φ(z|x)의 형태는 더 많은 자유도가 존재하지만, 저자들은 true posterior가 근사적으로 gaussian 형태를 취하며 대략 diagonal covariance를 가진다고 가정합니다.

 

이 경우, 근사 posterior를 diagonal covariance를 가진 multivariate guassian으로 둘 수 있게 됩니다. 근사 posterior의 평균 μ와 표준편차 σ는 encoding MLP의 output입니다. 즉 datapoint x와 variational parameter Φ에 대한 nonlinear function이라는 뜻입니다. ε이 standard normal distribution에서 sample된 값이라고 할 때, posterior로부터 sample된 z는 μ + ε ⊙ σ와 같이 표현될 수 있습니다(reparameterization trick). 여기서 ⊙는 element wise product를 의미합니다.

 

이 model에서는 p_Θ(z)와 q_Φ(z|x)는 gaussian이고, 위와 같은 형태의 식을 사용할 수 있게 됩니다.

 

최종적으로 나타내면 위와 같은 식으로 나타낼 수 있게 됩니다. multivariance gaussian distribution에 대한 KL divergence를 구하는 상태이므로 위와 같은 형태의 식으로 변환 가능합니다.

decoder term인 위 식에서 우변의 두번째 항은data의 type에 따라 Bernoulli든 Gaussian이든 결정하고 modeling하면 됩니다. 이미지의 경우 흑백 이미지를 생성한다면 bernoulli를 적용해도 됩니다.

 

Related work

AEVB(Auto Encoder Variational Bayes)은 directed probabilistic model(trained with a variational objective)와 auto-encoder의 연결성을 보여줍니다. linear auto-encoder와 특정 class를 생성하는 linear-gaussian model사이의 연결은 오래전부터 알려져왔습니다. PCA가 prior p(z) ~ N(0, I)와 조건부 확률 분포 p(x|z) = N(x; Wz, εI)로 이루어진 linear gaussian model의 경우, maximum-likelihood(ML)의 해결책으로 적합하다는 것을 보여줍니다. 특히 매우 작은 ε의 경우 적합함을 보여줍니다.

 

Experiments

저자들은 MNIST와 Frey Face dataset을 이용해 이미를 생성하는 모델을 학습했습니다. 그리고 variational lower bound와 추정된 marginal likelihood 측면에서 learning algorithm을 비교했습니다. encoder와 decoder의 hidden unit 수는 동일합니다. Frey Face data의 경우, continuous한 value로 이루어져 있기 때문에, decoder의 output에 sigmoid를 사용하여 평균을 0에서 1사이로 제약했습니다.

 

위와 같은 실험 결과를 얻을 수 있습니다. 위 결과를 보면 latent space의 차원을 다르게 설정하며 결과를 얻었습니다. 저자들이 제안한 방식이 더 빠르고 더 나은 결과를 얻는 것을 볼 수 있습니다. 흥미롭게도, 더 많은 latent variable이 overfitting을 유발하지 않는 것을 볼 수 있는데, 이는 lower bound의 regularizing에 의해 설명됩니다(KL divergence term을 이용).

 

위 실험 결과를 보았을 때도, 저자들의 model이 좋은 성능을 보이는 것을 알 수 있습니다.

 

conclusion

저자들은 continuous latent variable의 근사 추론을 효과적으로 하기 위해 variational lower bound estimator와 Stochastic Gradient VB(SGVB)를 소개했습니다. 제안된 estimator는 standard stochastic gradient method를 사용하여 쉽게 미분되고 최적화될 수 있습니다. independent and identically distribution(독립항등분포)인 dataset이고 각 datapoint가 continuous latent variable인 경우 저자들은 Auto-Encoding VB(AEVB)라는 효과적인 추론 및 학습 알고리즘을 소개했습니다. AEVB는 SGVB estimator를 이용하여 근사 추론 모델을 학습합니다.