데이터의 분포를 추정했을 때 얼마나 잘 추정한 것인지 측정하는 방법(두 분포가 얼마나 다른지)으로 KL Divergence와 Jesen-Shannon Divergence에 대해 알아보겠습니다.
KL Divergence
먼저 KL Divergence는 Kullback-Leibler Divergence의 줄임말입니다. 이는 정보 엔트로피를 이용해 비교가 진행되는 방식입니다. 그러다 보니 Relative entropy라고도 불립니다.
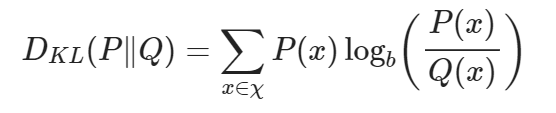
먼저 이산확률분포 P와 Q가 동일한 샘플 공간 χ에서 정의된다고 하면 KL Divergence 식은 위와 같이 정의됩니다. 위 식에서 사용된 log의 밑은 보통 e, 2, 10 중 하나를 사용합니다. 어떤 것을 사용하냐에 따라 정보량의 단위는 변경될 것입니다.
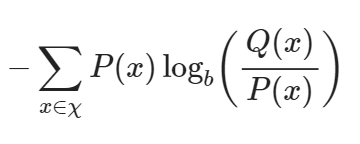
처음 식은 위와 같은 식의 형태를 띄고 log의 성질을 통해
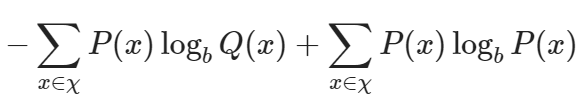
이와 같은 형태로 식이 전개될 수 있습니다. 위 식에서 ∑P(x)는 확률분포 P(x)에 대한 기댓값으로 치환할 수 있으며
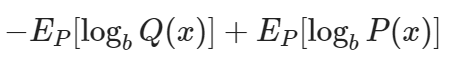
이와 같이 변경 가능합니다. 또한 이 식은
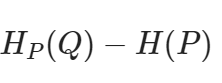
이와 같은 형태로 변경 가능합니다. 위 식에서 H_P(Q)는 P 기준으로 봤을 때의 Q에 대한 cross entropy를 의미하고 H(P)는 P에 대한 정보 entropy를 의미합니다. 즉 P(x)에 맞춰진 정보량을 보내야 할 자리에 Q(x)를 넣었을 때의 총 정보량과 P(x)를 보냇을 때의 정보량의 차이를 의미합니다.
식을 보면 알 수 있듯이 KL(P|Q)는 KL(Q|P)와 같지 않습니다. 즉 asymmetric합니다. KL(P|Q) = 0이라면 두 분포 P와 Q는 동일합니다. 그리고 KL(P|Q)는 항상 0보다 크거나 같습니다.
이런 KL Divergence를 이용해 그래프로 표현한다면
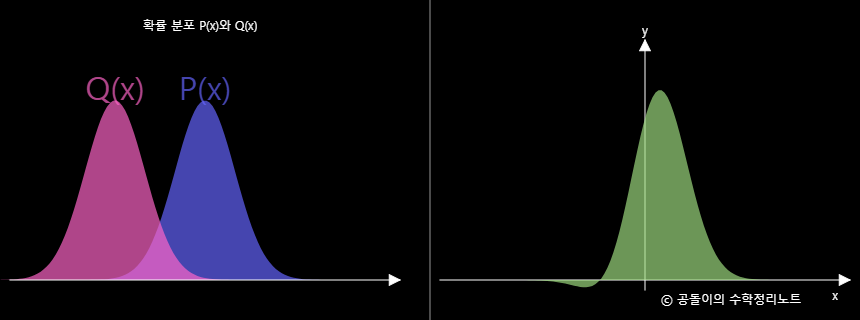
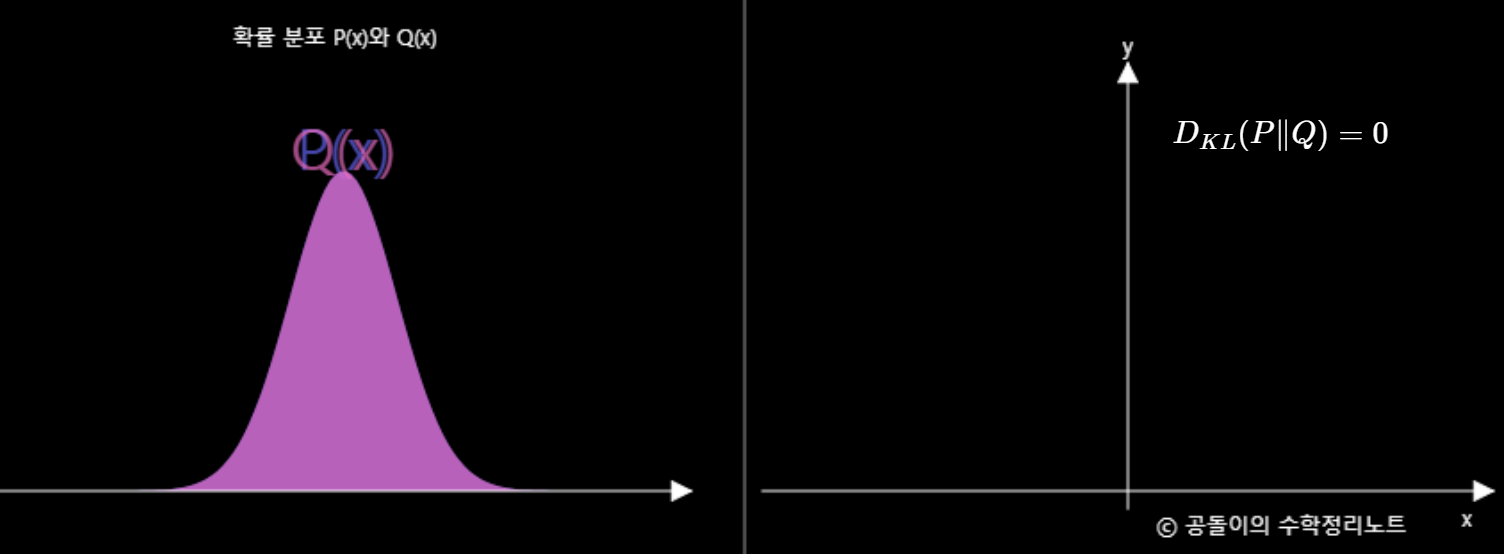
이와 같이 그릴 수 있습니다. 초록색 그래프의 넓이 합이 KL Divergence값이 됩니다.
Jensen-Shannon Divergence
KL Divergence는 assymmetric하기 때문에 이를 symmetric 하게끔 변경한 것이 Jensen-Shannon Divergence입니다.
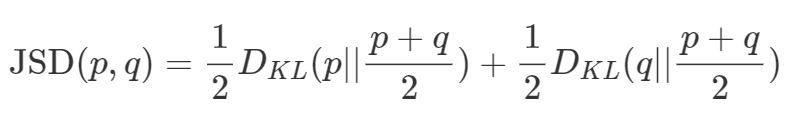
식은 위와 같습니다. 위에서 알아본 KL Divergence를 통해 JSD 식을 해석할 수 있습니다. JSD는 p와 q의 중간 값을 사용해 KL Divergence를 구하기 때문에 symmetric해지는 것을 볼 수 있습니다. 즉 JSD(p, q) = JSD(q, p)입니다. 이를 통해 두 확률 분포 사이의 거리(distance)의 역할을 할 수 있게 됩니다. 참고로 p = q인 경우 JSD의 값은 0이 됩니다.
'연구실 공부' 카테고리의 다른 글
| [ML] 2. MAP (0) | 2023.02.28 |
|---|---|
| [ML] 1. MLE (0) | 2023.02.28 |
| Contrastive Learning for Unpaired Image-to-Image Translation 논문 코드 (0) | 2023.02.13 |
| CycleGAN 논문 코드 (0) | 2023.02.07 |
| AutoEncoder(AE), Variant AutoEncoder(VAE) (0) | 2023.02.06 |



