해당 자료는 https://m.edwith.org/machinelearning1_17/intro 해당 강의에서 제공합니다.

강의에서 MLE, MAP를 설명하기 위해 압정 던지기를 예시로 설명해 주십니다. 압정이 앞이 나올 확률을 구하는 것이 목표로 하는 상황을 가정합니다.

우리의 예시는 2가지 경우만 존재합니다. 그렇기 때문에 binomial distribution을 사용합니다. 이산 확률 분포를 사용해 내용을 이어갑니다. 압정을 던지는 사건은 각 사건이 독립적이고 각 경우마다 동일한 확률 분포를 가지고 사건이 진행된다는 가정을 두고 진행합니다.
P(H)는 압정의 head가 나올 확률을 의미하고 이를 Θ로 표현합니다. 그럼 tail이 나올 확률은 1-Θ이 될 것입니다. 만약 우리가 5번 압정을 던지고 결과가 H, H, T, H, T이고 Θ확률로 head가 나온다면 P(D|Θ)는 Θ^3(1-Θ)^2이 됩니다. P(D|Θ)는 Θ가 주어졌을 때 D라는 data가 관측될 확률을 의미합니다.

우리의 가정은 '압정의 head가 나올 확률은 Θ다'라는 것입니다. 우리의 가정의 신뢰성을 높이기 위해서 우리는 최적의 Θ를 찾아야 합니다.
이제 여기서 MLE(Maximum Likelihood Estimation)가 등장합니다.
P(D|Θ)가 최대가 되는 Θ를 찾을 것이고 그 값을 Θ'으로 표현하겠습니다. 즉 우리가 관측한 data의 확률이 최대가 되는 Θ'을 찾는 것이 목표가 되고 이런 방식이 MLE입니다.
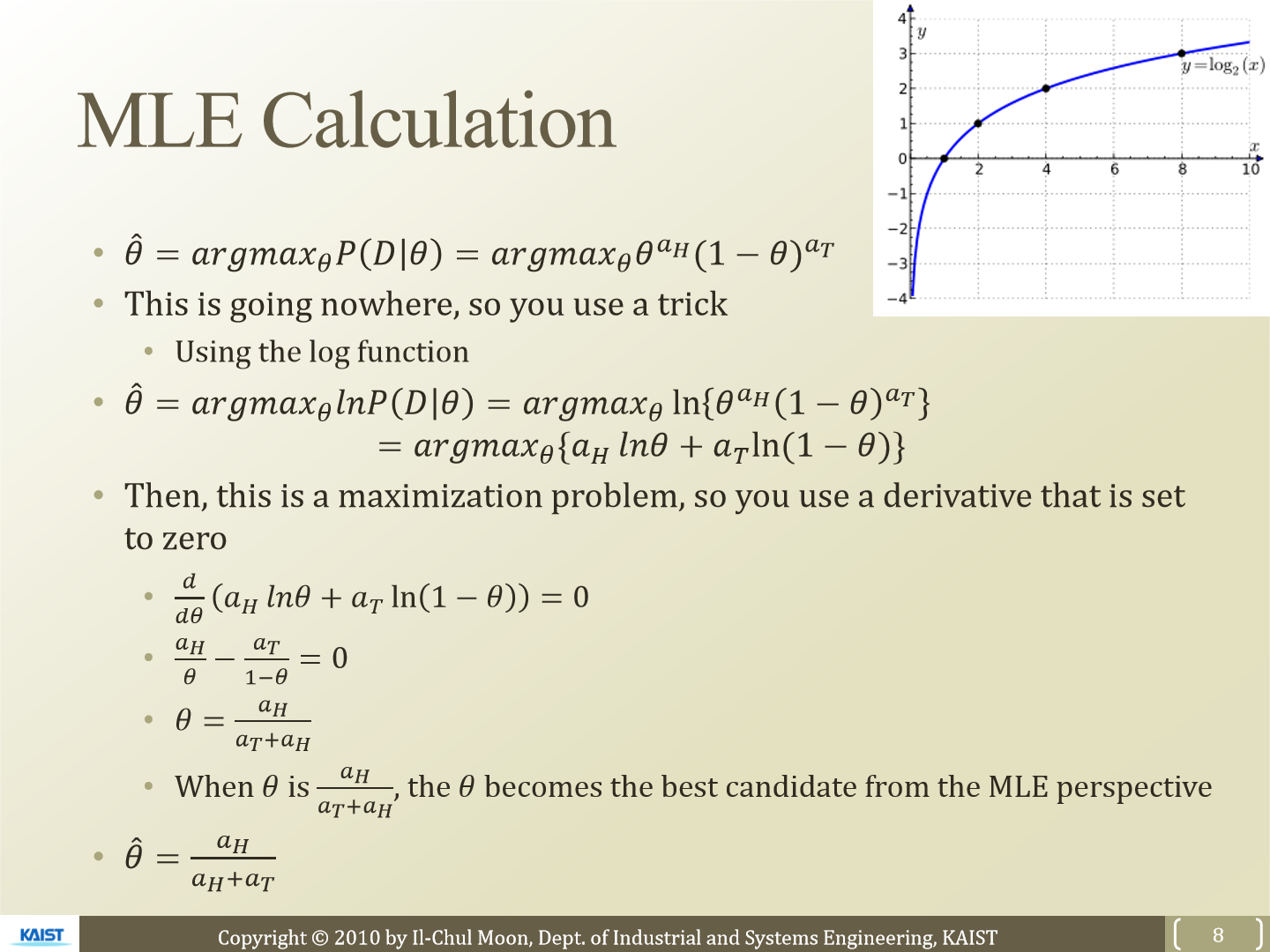
Θ'을 구하는 식을 그냥 다루기는 어렵기 때문에 log를 사용해 다룹니다. log는 monotonic하게 증가하는 function이니까 P가 최대가 되는 값은 logP가 최대가 되는 값과 같다고 볼 수 있습니다.
이제 log를 사용해 식을 표현하면 argmax_Θ{α_H x lnΘ + α_T x In(1 - Θ)}가 됩니다. 이제 이 식에서 argmax안에 있는 값이 최대가 되는 Θ를 찾는, optimize 하는 문제가 됩니다.
최대가 되는 Θ를 찾기 위해 식을 미분합니다. 결국 식이 최대가 되는 Θ는 α_H/(α_H + α_T)가 됩니다. Θ가 이와 같은 값을 갖는다면 MLE 관점에서 최적의 Θ를 찾은 것이 됩니다.

우리가 구한 Θ'은 추론을 한 값이지 official하게 최적의 값은 아닙니다. 만약 우리가 압정을 던지는 행위를 더 많이 진행한다면 우리가 구한 Θ'의 오차는 줄어들 것입니다.
Θ*를 official하게 true인 값이라고 할 때 Θ*와 Θ'의 값은 항상 0보다 큰 오차 ε가 생깁니다(trial error가 항상 존재하기 때문).
hoeffding's inequality를 사용해 우리가 구한 Θ'와 Θ*의 차이에 대한 절대값이 오차 ε보다 크거나 같을 확률을 대략적으로 구할 수 있습니다. 식은 위 그림과 같고 N은 던진 횟수를 의미합니다. 만약 오차 ε가 크다면 확률 값은 더 작아집니다. 또한 N이 커진다면 확률 값 역시 작아집니다.
'연구실 공부' 카테고리의 다른 글
| [ML] 3. Rule Based Machine Learning (0) | 2023.03.03 |
|---|---|
| [ML] 2. MAP (0) | 2023.02.28 |
| KL Divergence, Jensen-Shannon Divergence (0) | 2023.02.18 |
| Contrastive Learning for Unpaired Image-to-Image Translation 논문 코드 (0) | 2023.02.13 |
| CycleGAN 논문 코드 (0) | 2023.02.07 |



