먼저 speaker recognition(화자 인식)은 음성이 주어졌을 때, 해당 음성의 발화한 사람이 누구인지를 찾는 것입니다.
사람마다 고유한 음성 특징이 있습니다. 그래서 해당 음성 특징을 이용해 발화한 사람을 찾을 수 있습니다. 화자 인식은 크게 2가지로 분류됩니다.
speaker identification과 speaker verification입니다.
speaker identification의 경우, 음성이 input으로 들어왔을 때, 해당 음성의 발화자를 찾는 것입니다. multi class classification인 느낌입니다.
speaker verification의 경우, 음성이 input으로 들어왔을 때, 해당 음성이 등록된 발화자의 음성인지 분류하는 것입니다. binary classification인 느낌입니다.
음성은 2가지로 분류할 수 있습니다.
text-dependent와 text-independent입니다.
text-dependet speaker recognition은 정해진 문장 또는 단어를 발화한 음성을 가지고 speaker recognition하는 것입니다.
text-independent speaker recognition은 정해진 문장 또는 단어가 없이 다양한 text를 가지고 speaker recognition하는 것입니다.
음성 인식을 하는 과정을 보겠습니다.
먼저 input speech가 존재할 때, input speech에서 acoustic feature를 뽑아냅니다. frame 단위로 feature를 얻는데, MFCC, spectrogram 등의 형태로 feature를 뽑아냅니다.
해당 feature를 가지고 바로 분류하기엔 한계가 존재합니다. 화자의 상태에 따라 같은 화자여도 발화하는 방식이 달라지기도 하기 때문에, low level feature를 가지고 바로 분류하지 않습니다. 그리고 음성의 길이에 따라 frame의 수가 달라지기 때문에, text independent한 방식으로 분류하는 건 한계가 존재합니다.
따라서 low level feature를 변형시켜 사용합니다. low level feature를 이용해 utterance level feature를 추출(speech embedding)합니다. utterance level feature는 input recording sample 단위로 추출하며, 주어진 음성에 존재하는 다양한 acoustic feature pattern 혹은 speaker의 다양한 vocal tract pattern을 요약하는 역할을 합니다. sample 길이와 무관하게 고정된 크기의 utterance level feature가 추출되기 때문에, low level feature보다 유용합니다.
utterance level feature를 추출하는 방식으로, GMM(Gaussian mixture model) supervector, JFA(joint factor analysis), i-vector 등이 존재합니다.
추출한 utterance level feature를 가지고 유사도, 확률을 측정하여 최종 판단을 합니다.
speaker identification의 경우, 등록된 speaker들의 utterance level feature와 input recording의 utterance level feature를 비교하여 화자를 찾습니다.
GMM supervector
GMM(Guassian Mixture Model)과 GMM supervector에 대해 알아보겠습니다.
GMM은 data의 distribution을 단일 gaussian distribution이 아니라 여러 개의 gaussian distribution으로 표현하는 기법입니다.

수식으로 표현하면 이와 같습니다. 단순히 여러 개의 gaussian을 weighted sum(normal distribution에 weight π를 곱하며 더하는)한 모습입니다. weight π은 해당 distribution이 선택될 확률을 의미합니다. 그렇기 때문에 하나의 x_i에 대해서, weight π들의 합은 1이 되어야 합니다. GMM이 존재할 때, 어떤 x_i의 확률을 구하기 위해선, 각 gaussian의 probability를 구해 weighted sum하면 됩니다.
GMM을 학습하는 방법으로, MLE가 존재합니다. 각 data가 동일한 확률 distribution에서 다른 data와 independent하게 생성되었다고 가정하면(i.i.d.),

이와 같은 log likelihood를 maximize하는 Gaussian distribution들의 parameter를 찾으면 됩니다. 가장 data 분포를 잘 근사하는 model을 찾으면 됩니다. 하지만 MLE식을 미분하면 closed-form solution으로 정리되지 않기 때문에 다른 방식으로 GMM parameter를 학습해야 합니다. GMM도 lower bound를 maximize하는 방식으로 parameter를 update합니다. 보통 lower bound에 EM algorithm을 적용해 update합니다.
data의 분포를 여러 개의 cluster로 표현한다는 점에서, GMM은 k-means와 같은 clustering algorithm으로 생각할 수도 있습니다. 하지만, k-means algorithm은 하나의 sample이 하나의 cluster에만 mapping되는 hard-clustering이지만, GMM은 여러 개의 cluster(gaussian mixture)에 확률적으로 걸칠 수있기에 약간 다릅니다.
음성 인식에서의 GMM은 다음과 같이 사용할 수 있습니다.
우리는 MFCC, spectrogram과 같은 acoustic feature를 utterance level feature로 표현하고 싶은 상태입니다. acoustic feature에 GMM을 적용하여 서로 다른 음성 특징을 표현하는 soft cluster를 할 수 있게 됩니다. 즉, 화자의 발화 sample을 GMM에 넣으면, 해당 발화의 acoustic feature가 각자 해당하는 곳으로 clustering된다는 것입니다.
하지만 이를 위해선 화자를 잘 표현하는 GMM을 modeling해야 합니다. 그래야 어떤 발화가 input으로 들어왔을 때, 올바르게 clustering할 것입니다. 그렇기 위해선 한 화자가 발화한 여러 개의 sample이 필요한데, 쉽지 않습니다. 그리고 sample의 내용에 따라 편향된 clustering 결과를 보일 수도 있습니다.
이러한 문제를 해결하기 위해 등장한 것이 Universal Background Model(UBM)입니다. UBM은 최대한 다양한 화자 및 발음의 음성을 수집한 후 EM algorithm을 적용해 생성한 GMM입니다. 이상적인 UBM은 특정 화자나 발음에 편향되지 않은 GMM이라고 볼 수 있습니다. UBM이 존재한다면, 우리가 가진 특정 화자의 한정된 sample의 posteriori probability를 maximize하도록 UBM parameter를 update하면 됩니다(MAP adaptation이라고 합니다).

위 그림과 같이 UBM에 새로 주어진 data에 adaptation되는 speaker model을 만들면 됩니다. 화자의 sample이 assign 많이되는 UBM의 gaussian mixture는 많이 shifting되고, 나머지 gaussian mixture는 적게 shifting되거나 parameter를 그대로 사용합니다.
이렇게 구한 Gaussian mixture model의 parameter중 하나인 평균을 사용해 GMM supervector를 만듭니다. 즉, 각 gaussian distribution의 mean vector를 concat해 supervector를 만드는 것입니다.
즉 이렇게 구한 GMM supervector는 특정 화자의 음성이 가진 통계적 발화 pattern을 축약하여 표현한 vector라고 볼 수 있습니다. GMM supervector는 frame의 수에 따라 길이가 달라지지 않습니다. 즉, 하나의 GMM이면 하나의 supervector가 생성되며, 고정된 크기를 갖습니다. 이렇게 구한 GMM supervector를 utterance level feature로 사용할 수 있습니다.
GMM supervector에 SVM을 적용하거나 화자 분류를 위한 deep neural network를 사용하면 화자 인식을 할 수 있습니다.
eigenvoice vector
GMM supervector를 사용하면 효과적이긴 하지만 문제가 존재합니다.
GMM supervector는 mean vector들을 concat하여 획득되기 때문에, 차원이 너무 크다는 문제가 존재합니다. (acoustic feature의 차원 x gaussian distribution의 수) 크기의 차원이 됩니다.
또한 GMM supervector에는 speaker information을 제외한 session information, channel information 등 불필요한 정보들이 존재합니다.
이러한 문제를 해결하기 위해 여러 방식들이 등장했습니다. 그 중 하나가 eigenvoice vector입니다.

본래 eigenvoice adaptation는 speaker verification task가 아니라 speech recognition system을 sample수가 적은 화자에 대하여 adaptation 시키기 위해 제안된 기법입니다.
eigenvoice adaptation은 GMM supervector에 있는 speaker dependent variability(distribution이 퍼져있는 정도, 즉 speaker variability는 speaker information이 speech distribution에 미치는 영향)를 GMM supervector보다 작은 차원의 subspace로 project하는 것입니다.
UBM supervector와 GMM supervector 사이의 차이가 eigenvoice matrix라고 하는 speaker subspace입니다. 해당 speaker subspace로 project되는 latent variable을 speaker factor라고 합니다. speaker factor가 speaker의 특징을 표현해주는 factor라고 생각하면 됩니다. 즉, GMM supervector가 특정 화자의 음성을 이용하여 얻어졌을 때, GMM supervector와 UBM supervector의 차이는 해당 화자의 variability라고 할 수 있습니다. 해당 speaker variability를 분해하여 얻어지는 low-dim latent variable을 speaker variability를 표현하는 speaker factor라고 할 수 있습니다.
실제로 speaker factor와 eigenvoice matrix를 구할 때, GMM supervector를 직접 구하지 않습니다. UBM이 주어졌을 때 GMM supervector의 likelihood를 maximize하는 eigenvoice matrix를 EM algorithm으로 학습합니다.
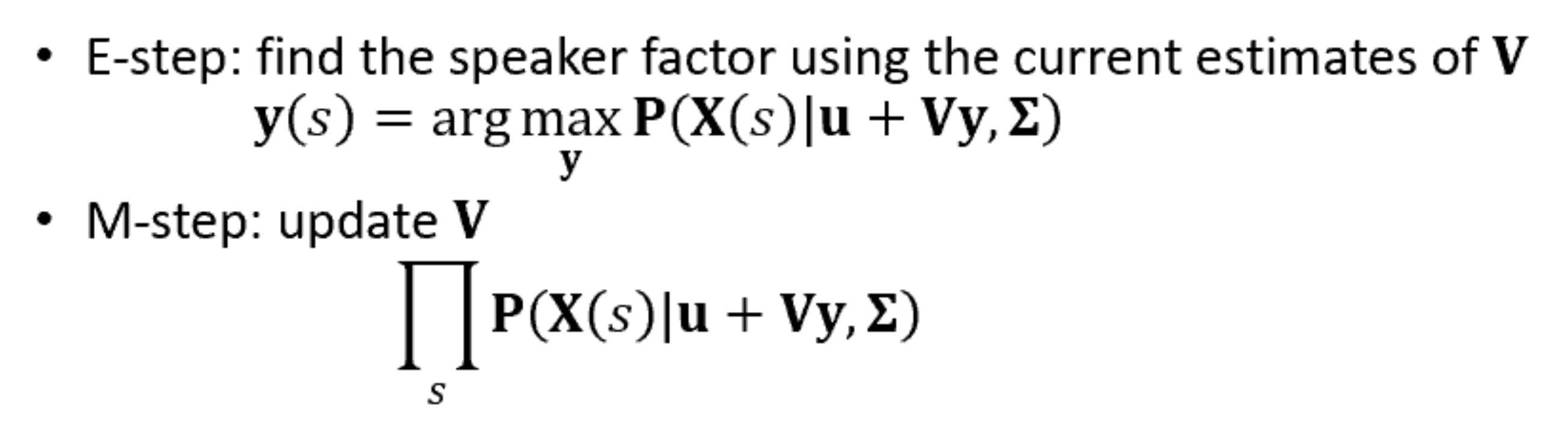
위 식과 같이 EM algorithm을 통해 train합니다. GMM supervector의 likelihood를 maximize하는 eigenvoice matrix(speaker subspace)를 찾는 과정입니다. 이와 같이 eigenvoice matrix를 구할 수 있고, eigenvoice matrix를 이용해 화자의 고유한 feature인 speaker factor를 extract하는데 사용됩니다.
Joint Factor Analysis(JFA)
이번엔 Joint Factor Analysis(JFA)를 보겠습니다. GMM supervector의 variability를 speaker factor, channel factor로 나누어 표현하는 방식입니다.

위처럼 speaker variability는 eigenvoice matrix와 speaker factor로 표현되고, channel variability는 eigenchannel matrix와 channel factor로 표현됩니다. 이 두 variability 외에 factor들을 residual factor로 표현합니다. 이렇게 GMM supervector를 나누어 표현합니다.
학습은 speaker subspace를 먼저 학습한 후, channel subspace, residual을 학습합니다.
JFA는 channel에 대한 정보를 따로 모델링하여 channel variability를 완화시키는 방식입니다. 하지만 channel factor에 여전히 speaker information이 남아있습니다. 즉, speaker factor만 이용하여 speaker의 feature를 온전히 표현하지 못하고 있다는 것을 의미하며, 이러한 한계를 극복하기 위해 등장한 것이 i-vector(identitiy vector)입니다.
I-Vector(identitiy vector)
channel factor에 speaker dependent information이 존재하니, 그냥 하나의 subspace로 speaker, channel 등 모든 variability를 표현하는 방식입니다. 음성 내의 모든 information을 저차원의 subspace(total variability subspace)에 표현하여 정보들이 섞여있지만 speaker information은 보존된 형태로 만듭니다.
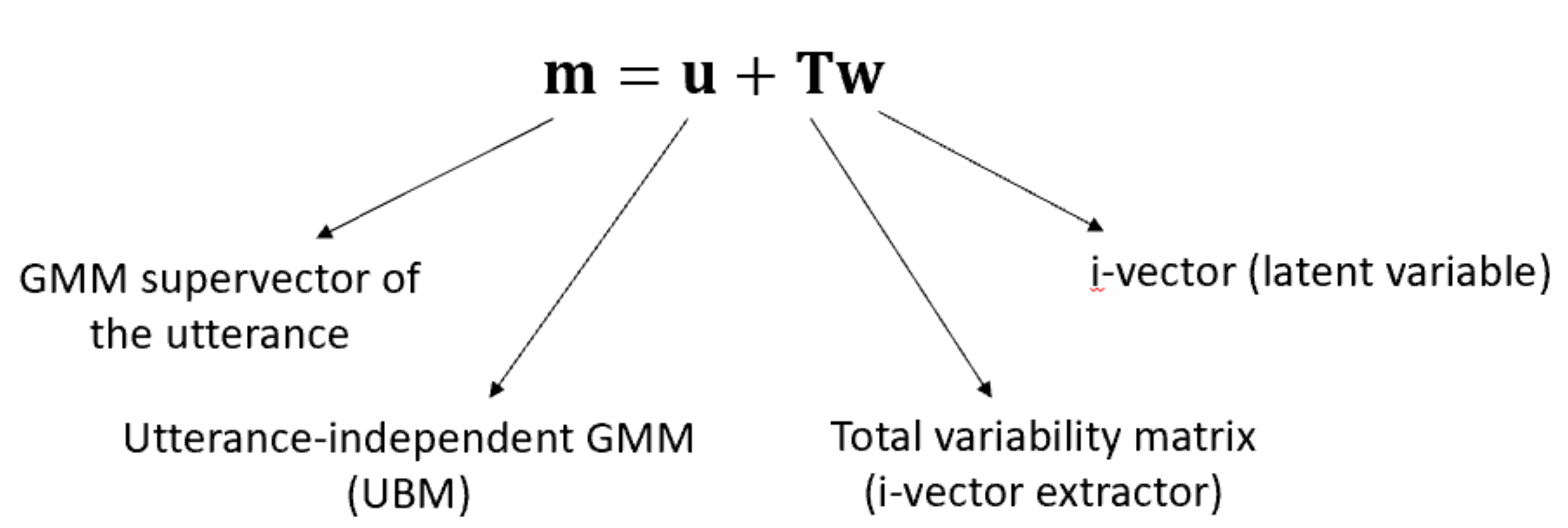
수식으로 표현하면 이와 같습니다. eigenvoice와 비슷한 형태입니다. 하지만 UBM의 모습이 다릅니다. eigenvoice를 구할 때는 target speaker에 independent한 GMM이였지만, i-vector를 구할 땐 각 utterance independent GMM입니다. 즉 각각의 발화가 서로 다른 speaker라고 생각을 한 형태입니다. 그렇기 때문에 각 발화에 대한 학습을 할때, w는 standard normal distribution에서 계속 새로 sampling하는 random vector가 되면 됩니다.
total variability matrix는 total variability covariance matrix에서 eigenvalue가 큰 eigenvector들로 구성된 matrix입니다. eigenvalue값이 크다는 것은 영향력이 크다는 뜻이고, eigenvector는 variability의 방향을 의미합니다. 그 후 speaker factor를 잘 표현하는 TVM을 만들도록 EM algorithm으로 학습됩니다. UBM supervector와 TVM*I-vector를 parameter로 하는 GMM이 얼마나 실제 GMM와 유사한지, 즉 likelihood를 구하여 maximize하는 방식으로 학습됩니다. 이는 i-vector와 data의 상관관계가 커지도록 학습되는 것을 의미합니다.
TVM은 기저 공간이 될 것이고 i-vector는 그 공간에 존재하는 latent variable로 보면 됩니다. 그래서 i-vector는 standard normal distribution의 형태이고 이 distribution이 GMM supervector와 UBM supervector의 차이를 가장 잘 설명할 수 있도록 하는 기저 공간 TVM을 찾아내는 과정이라고 볼 수 있습니다. 또는, total variability model이 있고 이 model의 parameter를 total variability matrix라고 하여, 해당 parameter를 update하면서 total variability model이 가장 GMM supervector와 UBM supervector의 차이를 잘 설명하도록 학습한다고 생각하면 됩니다.
학습된 TVM에서 i-vector를 구할 수 있고, i-vector는 GMM supervector보다 작은 차원을 갖기 때문에 연산량도 줄고 사용하기도 용이합니다.
나중에 i-vector 2개를 SVM with cosine kernel에 적용시키거나, cosine distance scoring을 통해 2개의 i-vector를 decision 합니다.
i-vector은 현재 speaker information만 존재하는 것이 아니기 때문에, 필요없는 information을 제거하는 과정을 거쳐야 합니다. i-vector는 GMM supervector에 비해 크기가 작기 때문에 다양한 feature compensation technique을 적용하여 nuisance effect를 제거할 수 있습니다.
먼저 within-class covariance normalization(WCCN)입니다. 이는 SVM 학습 과정에서 false acceptance의 expected error rate를 minimize하고 false rejecting의 expected error rate를 minimize합니다. classification error metric의 upper bound를 정의하여 error rate를 minimize합니다.

위 식을 통해 covariance matrix W를 구할 수 있습니다. 여기서 w_s bar는 speaker s의 i-vector 평균을 의미하며, S는 speaker 수를 의미합니다. w_i^s는 s라는 speaker의 각 발화에 대한 i-vector를 의미합니다. n_s는 speaker s의 발화 횟수를 의미합니다.
W^-1 = BB^T 형태로 분해가 가능하기 때문에 최종 SVM에 사용되는 cosine kernel은 아래와 같은 형태로 변형됩니다.

이를 통해 cosine kernel을 정규화하여 within-class covariance를 normalize할 수 있게 됩니다.
Linear discriminant analysis(LDA)입니다. 이는 주어진 화자의 모든 발화를 한 class라고 추정을 하면, LDA는 channel effect에 의해 발생되는 intra-class variance를 minimize하는 새로운 axes를 정의합니다. LDA를 통해 원하지 않는 방향은 제거할 수 있고 speaker 사이의 분산에 의해 제거되는 정보를 최소화할 수 있습니다. 다른 class를 분리할 수 있는 orthogonal axes를 찾는 방식입니다. axes는 서로 다른 class의 분산은 maximize하고 같은 class는 minimize해야합니다.
 |
 |
왼쪽 수식은 space direction v를 이용하는 ratio입니다. 서로 다른 class의 분산 S_b과 같은 class의 분산 S_w의 ratio를 의미합니다. 오른쪽 수식은 각 분산을 구하는 식입니다.

LDA는 이 ratio를 maximize해야 합니다. 저자들은 maximize하기 위해 projection matrix A를 정의했습니다. matrix A는 eigenvalue가 가장 큰 eigenvectors로 구성되어 있습니다. i-vector는 LDA에 의해 구해진 projection matrix A에 정의됩니다.
최종 cosine kernel은 아래와 같이 변형됩니다.

위 식에서 w1, w2는 i-vector입니다.
마지막으로 nuisance attribute projection(NAP)입니다. NAP는 nuisance direction을 제거할 수 있는 적절한 projection matrix를 찾는 algorithm입니다.
i-vector background에서 계산된 within-calss covariance 중 eigenvalue가 가장 큰 eigenvector를 기반으로 하는 channel space를 정의합니다. projection matrix는 channel complementary space에 직교하는 projection marix입니다. 해당 projection matrix는 결국 speaker에만 dependent하게 됩니다.

R은 직사각 matrix이며, 열은 k개의 eigenvectors로 이루어집니다. 이 eigenvector는 within-class covariance matrix와 동일한 best eigenvalues를 가지고 있습니다. eigenvector는 channel space를 정의합니다. 이러한 NAP를 cosine kernel에 적용하면

이와 같은 형태로 표현할 수 있습니다.
저자들은 cosine kernel을 사용하는 SVM 기반 system을 이용하여 i-vector 사이의 similarity를 구하는 방법과 target speaker의 i-vector와 test speaker의 i-vector의 cosine distance를 직접 계산해 decision score로 사용하는 방법을 제시했습니다.
LDA와 WCCN을 같이 사용했을 때 가장 좋은 결과를 얻었으며, cosine distance scoring 방식으로 진행했을 때는 speaker enrollment없이 진행가능하다는 장점도 보였습니다.
'연구실 공부' 카테고리의 다른 글
| [논문] Deep Neural Network Embeddings for Text-Independent Speaker Verification (0) | 2024.02.01 |
|---|---|
| [논문] Deep Neural Networks for Small Footprint Text-dependent Speaker Verification (0) | 2024.01.31 |
| [논문] Front-End Factor Analysis for Speaker Verification (0) | 2024.01.30 |
| 음성 인식 관련 용어 정리 (0) | 2024.01.28 |
| [논문] Auto-Encoding Variational Bayes (0) | 2024.01.19 |



